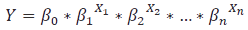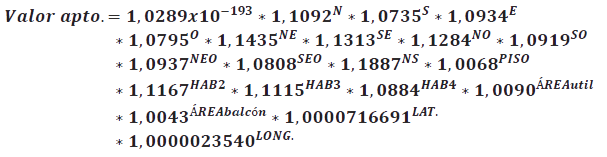Estimación de los efectos de la altura del piso y la orientación sobre el valor de los apartamentos

INTRODUCCIÓN
En los últimos años, explicar y/o predecir el valor de un inmueble ha requerido de herramientas, técnicas y métodos cada vez más precisos que intentan recoger de la forma más completa posible los elementos que aportan valor a dicho inmueble. Frecuentemente nos abocamos a desarrollar y/o detallar las variables tradicionales, sin embargo, una práctica cada vez más frecuente es la inclusión de nuevas variables (cualitativas o cuantitativas) que de forma objetiva y científica se ha determinado que sí generan efectos sobre el valor. En las principales urbes de Latinoamérica existen grandes bases de datos que asocian diversas variables que de acuerdo con cada entorno son importantes en el valor del inmueble, si con estas bases de datos creamos modelos matemáticos (econométricos), podríamos determinar si las variables que por nuestra experiencia entendemos que sí aportan valor, realmente lo hagan. Por ello, se pretende aportar una herramienta que recoja la influencia de las variables no tradicionales, se optimicen los dictámenes de valoración y se aumente la calidad del producto final.
I. EL PROBLEMA
I.1. PLANTEAMIENTO DEL PROBLEMA
El valor de los bienes inmuebles viene dado por la suma de los componentes parciales que contribuyen a interpretar la creación de dicho valor. Asimismo, las exigencias de los usuarios para adquirir un inmueble son cada vez más específicas, por ejemplo, en Chile una de estas características es la orientación, fenómeno que tal vez en otros países del continente no tenga mayor importancia. Debido a las estaciones del año (primavera, verano, otoño e invierno), la temperatura interna del inmueble y/o la proyección de la luz solar hacia él, hacen que la orientación del inmueble se traduzca en un plus o una contra al momento de ofertar o adquirir dicho inmueble. Ahora bien, a diario los propietarios, arrendatarios, corredores y avaluadores reconocen este fenómeno en combinación con la altura del piso; una particularidad mucho más tradicional donde normalmente se prefieren los inmuebles más altos sobre los más bajos, sin embargo, no se conoce una herramienta que cuantifique estos efectos al momento de determinar el valor de un inmueble. La actividad cotidiana de la valoración urbana nos obliga a realizar análisis univariantes (de una sola variable) con pocos datos (≤10), de forma “rápida y confiable”, ésta última pauta queda en entredicho cuando estudiando una sola variable no se tiene en cuenta el efecto de otras variables que no pueden ser introducidas de forma directa, para ello nos apoyamos en los modelos de homogeneización, donde intentamos ajustar o corregir los comparables para hacerlos más semejantes al inmueble tasado con el fin de realizar un mejor análisis de comparación directa, sin embargo, dichos factores no siempre tienen el suficiente sustento o en algunos casos son netamente arbitrarios, por lo que podemos incurrimos en graves errores, que se traducen en sobrevalorar o infravalorar un inmueble, siendo esto un detrimento a la hora de una garantía bancaria, una disputa judicial, entre otros escenarios. Por lo tanto, se plantea con base en la interpretación de un modelo econométrico de tipo multiplicativo la determinación de los efectos combinados de la altura del piso, la orientación, áreas asociadas, entre otros, en el cálculo del valor de los apartamentos ubicados en la comuna de Providencia, Chile.
II. BASES TEÓRICAS
II.1. MODELOS ECONOMÉTRICOS
Gujarati (2010), en su interpretación del análisis de los modelos econométricos, específicamente define que los modelos de regresión tratan del estudio de la relación de una variable dependiente respecto a unas variables independientes o explicativas, con el objeto de estimar y/o predecir un valor promedio de la primera en términos de los valores conocidos de las últimas. Dentro de los modelos econométricos existen los de tipo multiplicativo, donde en ellos se puede ver de forma directa la relación porcentual en la que aumenta o disminuye una variable en función del valor que tome, un ejemplo de este tipo de modelos es la regresión exponencial múltiple, cuya ecuación general se escribe como sigue:
En una adaptación de lo descrito por Guijarro (2013) se tiene que Y es la variable dependiente (el valor de los inmuebles en nuestro caso), ß0 es la constante o intercepto, Xi es la i-ésima variable explicativa y ßi es el coeficiente asociado a la i-ésima variable explicativa. El coeficiente ß0 se interpreta como el valor de la variable dependiente cuando todas las variables independientes son igual a cero. El coeficiente ßi se interpreta como el incremento o disminución porcentual experimentado por la variable Y cuando la variable Xi se incrementa en una unidad, manteniendo constantes el resto de las variables, siguiendo el principio ceteris paribus. Asimismo, los modelos de regresión múltiple (de dos o más variables) tienen diversos medios de verificación respecto a su capacidad explicativa y predictiva, por ejemplo, el coeficiente r2 ajustado y la validación cruzada. El estudio de otros factores complementarios tales como el p-value o nivel de significancia global del modelo y de las variables, la multicolinealidad, la normalidad, la heterocedasticidad y la eliminación de outliers por residuos estándares y/o por distancia Mahalanobis, deben ser considerados durante el análisis de los modelos de regresión. Estos conceptos son explicados suficientemente por el autor citado en su texto.
III. MARCO METODOLÓGICO
III.1. MUESTRA DE DATOS COMPARABLES
III.1.1. Obtención de la muestra
La fuente de donde se obtuvo la muestra son las publicaciones de ofertas de inmuebles en toda la comuna. Esta información fue extraída del portal web www.portalinmobiliario.com. La muestra es de corte transversal referida a consulta realizada en mes de junio de 2017. La muestra de datos comparables registrados para el período considerado está compuesta por mil trescientos treinta y cuatro (1334) referenciales o datos comparables con la siguiente información: índice / código del proyecto PI, No de habitaciones, No de baños, identificación del apartamento, altura del piso, orientación, área útil (m2), área de balcón (m2), área total (m2), precio de venta (UF).
III.1.2. Ubicación georeferencial de los inmuebles
Una vez definida la muestra, se ubicaron los edificios a los que pertenecen, sobre un plano general de la comuna. Para ello, se utilizó como herramienta el sistema de información geográfica QGIS.
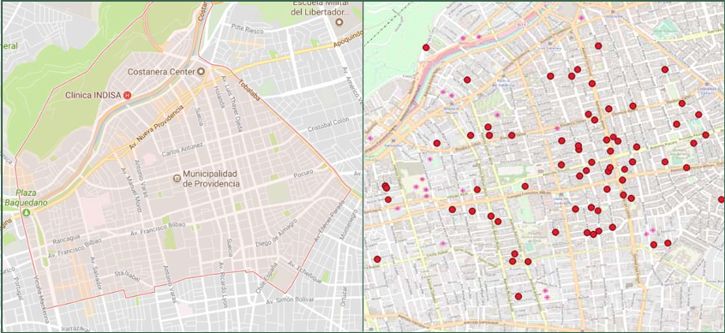
Figura 1. Límites de la comuna de Providencia y georeferencia de los datos comparables. Fuente: Propia
III.2. DETERMINACIÓN DEL MODELO ECONOMÉTRICO DE REGRESIÓN MÚLTIPLE
III.2.1. Definición de las Variables
Las variables que forman parte del análisis de regresión múltiple se componen de dos tipos: las dependientes y las independientes. De acuerdo con lo anterior, las variables fueron definidas como sigue:
Dependiente: Valor de los Apartamentos
Independientes: #Habitaciones, #Baños, Área Útil (interior / espacio cerrado) – Área de Terraza (balcón / espacio abierto) – Altura del piso – Orientación – Latitud (UTM) – Longitud (UTM)
Asimismo, las variables cuantitativas o también llamadas de tipo numéricas a introducir en el modelo serán: #Habitaciones, #Baños, Área Útil, Área de Terraza y Altura de piso, mientras que en el caso de la Orientación al ser de naturaleza cualitativa requerirá una transformación adicional a dummy para poder introducir dicha cualidad al modelo matemático. Guijarro (2013) y Dantas (2002) describen ampliamente estos procedimientos en sus textos. En función de lo anterior, las variables #Habitaciones, #Baños y Orientación fueron transformadas a “variables ficticias” según el principio G-1. Entonces, si una variable puede tomar 4 valores o niveles ordinales; se dice que posteriormente por cada variable ordinal con n niveles diferentes, se deben definir o construir n - 1 variables binarias (Guijarro 2013, p.80), por lo tanto, para el caso del No de Habitaciones se deben crear tres (3) variables binarias, las variables a crear pueden verse en la Tabla No 1.
| Variable ordinal: | Toma valores iguales a: | Número de niveles: | Variables binarias creadas: |
|---|---|---|---|
| #Habitaciones | 1, 2, 3, 4 | 4 | Hab2, Hab3, Hab4 |
| #Baños | 1, 2, 3 | 3 | Baños2, Baños3 |
| Orientaciones | N, S, E, O, NE, SE, NO, SO, NEO, SEO, NSE, NS, NSO | 13 | N, S, E, O, NE, SE, NO, SO, NEO, SEO, NSE, NS |
Tabla 1. Definición de las Variables Binarias Ordinales. Fuente: Propia
Por ejemplo, si un comparable tiene un valor de No de Habitaciones igual a tres (3), se dice que Hab2 = 0, Hab3 = 1 y Hab4 = 0. Las variables destacadas en “negrita”, se les conoce como variables de referencia o variables base, con el cual se compararán el resto de las variables binarias.
IV. ANÁLISIS DE RESULTADOS
IV.1. MODELO DE REGRESIÓN EXPONENCIAL MÚLTIPLE
La muestra utilizada para construir el modelo de regresión de la comuna está compuesta por 1334 datos en total. A continuación, se observa el comportamiento de las variables independientes de forma particular respecto a la variable dependiente y su distribución por espacios interiores:
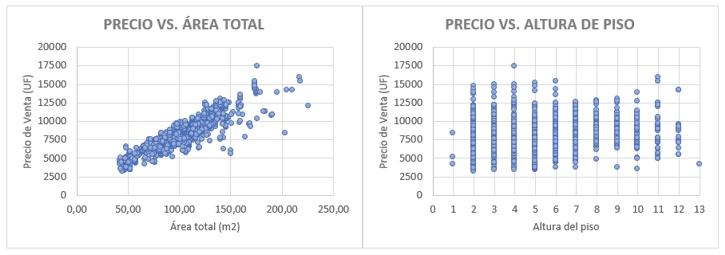
Gráfica 1. Comportamiento del precio respecto a las variables área total y altura de piso. Fuente: Propia
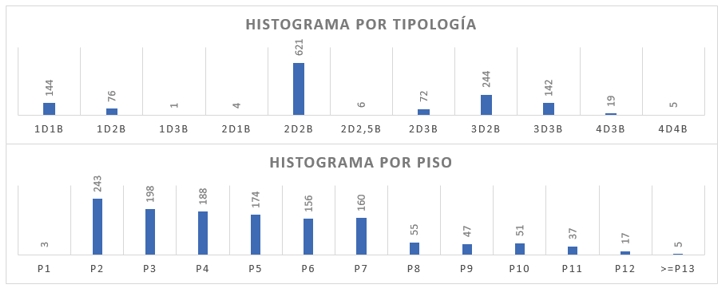
Gráfica 2. Distribución de los datos por tipología y altura de piso. Fuente: Propia
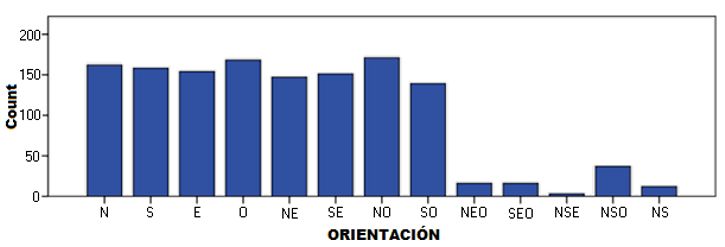
Gráfica 3. Distribución de los datos por orientación. Fuente: Propia
La ecuación que explica el comportamiento del mercado de apartamentos en la comuna es como sigue:
IV.2. INTERPRETACIÓN DEL MODELO Y SUS RESULTADOS
Del modelo expuesto en el apartado anterior, podemos identificar e interpretar los siguientes comportamientos siguiendo el concepto ceteris paribus:
-
- Si el apartamento tiene una orientación Nor-Este (NE), el valor del apartamento aumenta en promedio en toda la comuna en un 14,35% respecto a la orientación de referencia NorteSurOeste (NSO), por otro lado, una de las peores orientaciones resulta cuando el apartamento tiene una orientación Sur (S), donde el valor del apartamento aumenta sólo en 7,35%.
- Por cada piso que aumenta el apartamento, el valor del apartamento aumenta en 0,68%; es decir, un apartamento en el piso 12 vale 6,80% más que un apartamento que esté en el piso 2.
- Tomando como referencia un apartamento de 1 dormitorio, un apartamento de 2 habitaciones vale 11,67% más, uno de 3 habitaciones vale 11,15% más y uno de 4 habitaciones vale 8,84% más, respectivamente. Es lógico, en este mercado un apartamento con más de 1 habitación, a medida que se aumenta el número de habitaciones, pero con los mismos metros cuadrados, se genera un efecto negativo de “hacinamiento”.
- Por cada metro cuadrado útil que aumenta el inmueble, su valor aumenta 0,9%. La relación de crecimiento de valor entre el área de balcón y el área útil es de 0,477 en promedio en toda la comuna de Providencia, lo que confirma la práctica común de valorar en 50% el área abierta respecto al área privada.
- Respecto a la ubicación, el valor de los apartamentos aumenta a medida que aumenta su latitud y su longitud, esto tiene coherencia puesto que a medida que aumenta la latitud se acerca a la zona comercial y más atractiva de la comuna; y a medida que aumenta la longitud se observa el cambio de segmento socioeconómico, desde la frontera con la comuna de Santiago hacia la frontera con la comuna de Las Condes, por lo que la interpretación económica del modelo coincide con la lógica del mercado actual en el sector.
IV.3. INTERPRETACIÓN DEL MODELO Y SUS RESULTADOS
El coeficiente de determinación r2 es igual a 0.9234. Los outliers o datos atípicos de este modelo se identificaron vía residuos estándares (ZRE ≥ 3) y vía distancia Mahalanobis (MAH > 300), de un total de 1334 datos se encontraron 17 datos atípicos que representan el 1,27% de la muestra (cumpliéndose la condición de que la cantidad recomendada de outliers identificados debe ser menor al 5% del total de la muestra). El modelo es significativo globalmente (F >> Fo), además de que todas las variables son significativas al cumplirse la condición Sig. < 0,05. La variable #Baños fue retirada por presentar multicolinealidad respecto al Área útil. No se observa alguna tendencia clara que indique la presencia de heterocedasticidad, por lo que el modelo es homocedástico en toda su extensión. Finalmente, se observa la condición de normalidad en el histograma de residuos tipificados (Ver Gráfica No4).
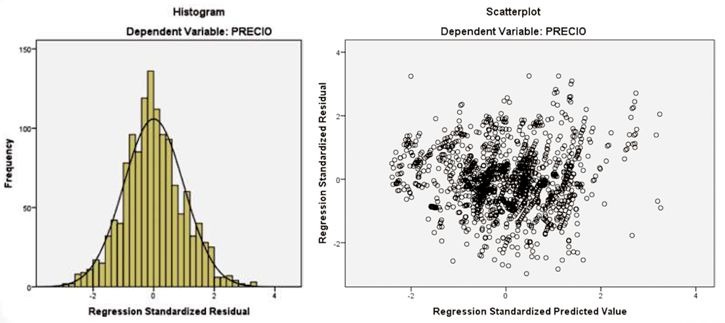
Gráfica 4. Histograma de residuos tipificados y Diagrama de dispersión de los residuos tipificados vs. valores calculados tipificados. Fuente: Propia
V. CONCLUSIONES
La exigencia por conocer y analizar el comportamiento de las cualidades propias o externas al inmueble se hacen cada vez mayor, dependiendo del país, la provincia o el sector de la ciudad, las variables que son importantes en una, tal vez no lo sean en otra, de ahí la gran dinámica del mercado. El modelo econométrico nos ha permitido ver la dinámica general de una comuna (municipio) de la ciudad de Santiago de Chile, donde tomando como premisa las variables altura de piso, su orientación, áreas asociadas, entre otras variables, se pudo observar que sí indicen sobre el valor de los inmuebles y que dentro de las alternativas o escenarios que tomen dichas variables serán determinantes para que aumenten o disminuyan el valor de una forma importante. Con la finalidad de mejorar los dictámenes de valoración y de crear inquietud entre los tasadores deben considerarse los efectos de estas variables combinadas, puesto que en el día a día los análisis univariantes respecto al área total del inmueble no son suficientes para recoger lo que el resto aporta al valor. Como resultado de este trabajo, se generó un modelo de regresión exponencial múltiple que nos ayudó a interpretar de manera porcentual los efectos que cada una de las variables generan sobre los inmuebles. El proceso metodológico puede ser aplicado para cualquier otra comuna de Chile o de otro país, donde haya suficientes datos, sin embargo, cabe destacar que los modelos y ecuaciones generados en el presente trabajo son únicamente aplicables en la comuna de Providencia en la ciudad de Santiago de Chile.
REFERENCIAS BIBLIOGRÁFICAS
-
- Camacaro M. (2016). El método contributivo en los avalúos inmobiliarios. Miguel Camacaro Ediciones, Venezuela.
- Dantas R. (2002). Ingeniería de tasaciones: Una introducción a la metodología científica. Miguel Camacaro Ediciones, Venezuela.
- Guijarro F. (2013). Estadística aplicada a la valoración (1a ed.). Universitat Politècnica de València, España.
- Gujarati D. y Porter D. (2010). Econometría (5a ed.). McGraw Hill Interamericana, S.A., México.• Gujarati D. y Porter D. (2010). Econometría (5a ed.). McGraw Hill Interamericana, S.A., México.• Gujarati D. y Porter D. (2010). Econometría (5a ed.). McGraw Hill Interamericana, S.A., México.